多层感知机 是最简单的深度网络，由多层神经元组成，每一层与它的上一层相连，从中接收输入；同时每一层也与它的下一层相连，影响当前层的神经元。本章还涉及许多基本的概念介绍，包括过拟合、欠拟合、模型选择、数值稳定性、参数初始化以及权重衰减和暂退法等正则化技术。

1. 多层感知机

1.1 简介

在第三章中涉及了线性回归和 softmax 回归，并在线性的背景下使用 Pytorch 进行了简单实现，这两个简单的回归基于第三章中介绍的 仿射变换，即一个带有偏置项的线性变换，但是，在实际生活中，线性 是一个非常强的假设。

我们或许有理由说一个人的年收入与其贷款是否违约具有负向线性相关性，但对于第三章章讨论的图像分类问题，就很难认为某个像素点的强度与其类别之间的关系仍是线性的。因此，我们选择构建一个深度神经网络，通过 隐藏层 的计算为我们的数据构建一种 表示，这种表示可以考虑特征之间的交互作用，在表示上，我们再建立一个线性模型用于预测可能是合适的。

通过在网络中加入一个或多个隐藏层，配合激活函数，我们便可以克服线性模型的限制，使其能处理更普遍的函数关系。最简单的方式就是将许多全连接层堆叠在一起，每一层都输出到其上面的层，直到生成最后的输出。我们可以把前 $L-1$ 层看作表示，最后一层看作线性预测器。这种架构通常称为 多层感知机 (multilayer perceptron)，通常缩写为 MLP。一般多层感知机的架构如下图所示：

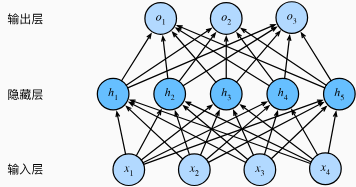
多层感知机

这个多层感知机有 4 个输入，3 个输出，其隐藏层包含 5 个隐藏单元。输入层不涉及任何计算，因此，这个多层感知机中的层数为 2。由于隐藏层和输出层都是全连接的，每个输入都会影响隐藏层中的每个神经元，而隐藏层中的每个神经元又会影响输出层中的每个神经元。

以 $\bold{X}\in\mathbb{R}^{n\times d}$ 来表示 $n$ 个样本的小批量，其中每个样本具有 $d$ 个输入特征。对于具有 $h$ 个隐藏单元的单隐藏层多层感知机，用 $\bold{H}\in\mathbb{R}^{n\times h}$ 表示隐藏层的输出，称为 隐藏表示 (hidden representations)，隐藏层变量 (hidden-layer variable) 或 隐藏变量 (hidden variable)。对于全连接的隐藏层和输出层，有隐藏层权重 $\bold{W}^{(1)}\in\mathbb{R}^{d\times h}$ 和隐藏层偏置 $\bold{b}^{(1)}\in\mathbb{R}^{1\times h}$ 以及输出层权重 $\bold{W}^{(2)}\in\mathbb{R}^{h\times q}$ 和输出层偏置 $\bold{b}^{(2)}\in\mathbb{R}^{1\times 1}$。由此便可以计算单隐藏层多层感知机的输出： $$ \begin{align*} \bold{H} &= \bold{XW}^{(1)} + \bold{b}^{(1)} \cr \bold{O} &= \bold{HW}^{(2)} + \bold{b}^{(2)} \cr \end{align*} $$

但是，上述网络只是两次线性仿射变换，本质上仍是仿射变换，并未比一次线性变换带来更多的信息，我们可以证明，任意与如上网络类似的多层感知机，只需合并隐藏层，就可以产生等价的单层模型。

那么，如何使多层感知机发挥更强的功能呢？答案是：在仿射变换之后对每个隐藏单元应用 非线性的激活函数 (activation function) $\sigma$，激活函数的输出 $\sigma(\cdot)$ 称为 激活值 (activation)。此时，多层感知机的计算方式为： $$ \begin{align*} \bold{H} &= \sigma(\bold{XW}^{(1)} + \bold{b}^{(1)}) \cr \bold{O} &= \bold{HW}^{(2)} + \bold{b}^{(2)} \cr \end{align*} $$

1.2 激活函数

激活函数 (activation function) 过计算加权和并加上偏置来确定神经元是否应该被激活，将输入信号转换为输出的可微运算，大多数激活函数都是非线性的。下面简要介绍一些常见的激活函数。

1.2.1 ReLU

修正线性单元 (Rectified linear unit，ReLU)，实现简单，同时在各种预测任务中表现良好。ReLU 提供了一种非常简单的非线性变换，对于给定元素，ReLU 函数被定义为该元素与 0 的最大值： $$ ReLU(x) = \max(x, 0) $$

即：ReLU 函数通过将相应的活性值设为 0，仅保留正元素并丢弃所有负元素。该函数是分段线性的。当输入为负时，ReLU 函数的导数为 0，而当输入为正时，ReLU 函数的导数为 1。注意，当输入值精确等于 0 时，ReLU 函数不可导。此时，我们默认使用左侧的导数，即当输入为 0 时导数为 0。

PyTorch 中可以设置输入为负时，ReLU 函数的导数值。且由于 ReLU 函数倒数为常数，其可以有效缓解梯度消失、梯度爆炸问题。

ReLU 函数的诸多变体，如 参数化 ReLU (parameterized ReLU, pReLU) 也经常使用。 $$ pReLU(x) = \max(0, x) + \alpha\min(0, x) $$

1.2.2 sigmoid

sigmoid 通常称为 挤压函数 (squashing function)，它将范围在 $(-\infty,\infty)$ 上的任意输入压缩到区间 $(0,1)$ 上的某个值： $$ sigmoid(x)=\frac{1}{1+\exp(-x)} $$

sigmoid 函数是一个平滑的、可微的阈值单元近似。当我们想要将输出视作二元分类问题的概率时，sigmoid 被广泛用作输出单元上的激活函数，它可以视为 softmax 的特例。

sigmoid 在隐藏层中已经较少使用，它在大部分时候被更简单、更容易训练的ReLU所取代。

sigmoid 函数的导数为： $$ \frac{d}{dx}sigmoid(x)=\frac{\exp(-x)}{(1+\exp(-x))^2}=sigmoid(x)(1-sigmoid(x)) $$

1.2.3 tanh

tanh (双曲正切) 函数也可以将范围在 $(-\infty,\infty)$ 上的任意输入压缩到区间 $(0,1)$ 上的某个值： $$ tanh(x) = \frac{1-\exp(-2x)}{1+\exp(-2x)} $$

sigmoid 和 tanh 在输入接近于 0 时都接近于线性变换，但 tanh 函数的斜率更大。

tanh 函数的导数为： $$ \frac{d}{dx}tanh(x)=1-tanh^{2}(x) $$

2. 实现一个多层感知机

仍使用手写数字数据集 Fashion-MNIST。

2.1 从零实现

import torch
from torch import nn
from d2l import torch as d2l

# 读取数据
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

# 隐藏层个数一般设置为 2 的幂次，因为计算机的内存分配使用字节，这样方便计算。
num_inputs, num_outputs, num_hiddens = 784, 10, 256

W1 = nn.Parameter(
    torch.randn(
        num_inputs, num_hiddens, requires_grad=True
    ) * 0.01
)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(
    torch.randn(
        num_hiddens, num_outputs, requires_grad=True
    ) * 0.01
)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))

params = [W1, b1, W2, b2]

# 激活函数
def relu(X):
    a = torch.zeros_like(X)
    return torch.max(X, a)

# 模型
def net(X):
    X = X.reshape((-1, num_inputs))
    H = relu(X @ W1 + b1)  # 这里“@”代表矩阵乘法
    return (H @ W2 + b2)

# 损失函数
loss = nn.CrossEntropyLoss(reduction='none')

# 训练
num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)

2.2 简介实现

# 模型
net = nn.Sequential(
    nn.Flatten(),
    nn.Linear(784, 256),
    nn.ReLU(),
    nn.Linear(256, 10)
)

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights)

# 训练
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=lr)

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)