多因子绩效归因
1. 摘要
投资组合的业绩归因可以分为 收益归因 和 风险归因 两个部分,而归因又可以基于净值或持仓进行。本文主要基于 持仓数据 对组合的业绩归因进行探讨。
在组合收益归因方面,主要有以下部分:
- 基于 Brinson 模型
- 经典版 BHB (Brinson, Hood and Beebower) 模型:将组合超额收益分解为配置收益、选股收益和交互收益 3 部分。
- 改进版 BF (Brinson and Fachler) 模型:引入行业超额收益,将组合超额收益分解为配置效应和选股效应两个部分。
- 基于多因子模型
- 基于行业的多因子收益归因:与自下而上的 Brinson 模型完全一致。
- 基于行业和风格的多因子收益归因:同时对行业和风格上的配置进行分析。
在组合风险归因方面,主要基于多因子模型:
- 单一波动分解法:单独考虑每个因子,计算简单,但忽略因子之间的协同影响,且不具可加性。
- 边际风险分解法:将组合风险分解为因子暴露度与因子边际风险贡献的乘积,然而偏导数的概念相对模糊,指导意义不强。
- 三要素分解法:将风险分解为因子暴露 ($x$)、因子波动 ($\sigma$) 和因子-组合相关系数 ($\rho$),对风险的分解更为透彻,更有利于投资经理对风险进行控制。
2. 基于 Brinson 模型的组合收益归因
2.1 经典 BHB 模型
BHB 模型将投资组合的超额收益率分解为 配置收益、选股收益和交互收益 三个部分,其基本框架如下图所示,其中红色渲染部分表示投资组合的超额收益。
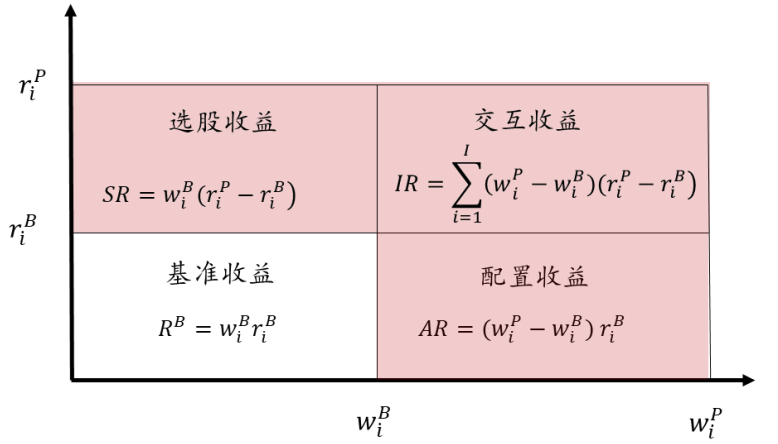
从行业配置的角度而言,假设 $w_{i}^{P}, w_{i}^{B}$ 分别表示投资组合和基准组合中行业 $i$ 的权重,$r_{i}^{P}, r_{i}^{B}$ 分别表示投资组合和基准组合中行业 $i$ 的收益率,那么投资组合的收益率 $R^{P}$ 和基准组合的收益率 $R^{B}$ 就可以表示为: $$ \begin{align*} R^{P}&=\sum_{i=1}^{I}w_{i}^{P}r_{i}^{P}, where\sum_{i=1}^{I}w_{i}^{P}=1 \cr R^{B}&=\sum_{i=1}^{I}w_{i}^{B}r_{i}^{B}, where\sum_{i=1}^{I}w_{i}^{B}=1 \end{align*} $$
其中,$I$ 表示行业个数。此时,投资组合超额收益 $R^{A}$ 即可表示为: $$ R^{A}=R^{P}-R^{B}=\sum_{i=1}^{I}w_{i}^{P}r_{i}^{P} - \sum_{i=1}^{I}w_{i}^{B}r_{i}^{B} $$
BHB 模型将组合超额收益拆解为 配置收益 (Allocation Return, AR)、选股收益 (Selection Return, SR) 和 交互收益 (Interaction Return, IR) 三部分,即: $$ \begin{align*} R^{A} &= AR+SR+IR \cr AR &= \sum_{i=1}^{I}(w_{i}^{P} - w_{i}^{B})r_{i}^{B} \cr SR &= \sum_{i=1}^{I}w_{i}^{B}(r_{i}^{P} - r_{i}^{B}) \cr IR &= R^{A} - AR - SR = \sum_{i=1}^{I}(w_{i}^{P} - w_{i}^{B})(r_{i}^{P} - r_{i}^{B}) \end{align*} $$
- 配置收益 (AR) 等于投资组合在每个行业上的超额权重与基准行业收益率的乘积 (AR = 超额权重 × 基准行业收益率),表示在行业内部不进行任何选股操作,持有与基准组合完全相同的行业,并通过超配收益为正、低配收益为负的行业所能够获取的超额收益。
- 选择收益 (SR) 等于基准权重与投资组合在行业上超额收益率的乘积 (SR = 基准权重 × 行业超额收益) ,表示在组合中保持每个行业权重与基准指数行业权重完全一致,通过行业内部的选股操作所能够获取的超额收益。
- 交互收益 (IR) 等于超额权重与超额收益的乘积 (IR = 超额权重 × 超额收益),表示由配置和选股共同产生的超额收益。
本文的所有示例都是按照行业进行划分的,但 Brinson 模型的应用远不止于此。对于大类资产配置的投资者而言,他可以将收益拆解到股票、债券、现金、基金和衍生品等不同类别的大类资产配置和选择带来的收益,对于债券投资者而言,他可以将超额收益拆解到企业债、信用债、利率债、国债等不同债券类别的配置和选择带来的收益。
BHB 模型存在的不足:
- 配置效应 $AR = \sum_{i=1}^{I}(w_{i}^{P} - w_{i}^{B})r_{i}^{B}$ 中,BHB 模型 认为超配行业绝对收益为正的行业即可获得配置效应,但若某些行业只是具有正收益,但却未能胜过基准组合,即:$0 < r_{i}^{B} < R^{B}$,那么超配此类行业显然不是完全成功的。
- 选择效应 $SR = \sum_{i=1}^{I}w_{i}^{B}(r_{i}^{P} - r_{i}^{B})$ 中,当投资组合中某行业相对基准行业存在超额收益,但投资组合对该行业的权重配置低于基准权重配置,即:$w_{i}^{P} < w_{i}^{B}$,若仍按基准权重来计算选择效应,结果会存在一定高估。
- 交互效应 $IR = \sum_{i=1}^{I}(w_{i}^{P} - w_{i}^{B})(r_{i}^{P} - r_{i}^{B})$ 的概念相对模糊,配置效应是对绝对收益为正的行业的超配、对绝对收益为负的行业的低配带来的收益,选股效应是对超额收益为正的个股的超配、对超额收益为负的个股低配带来的收益,但交互项收益部分很难从操作层面去解释,为组合的管理带来了难题。
2.2 改进版 BF 模型
BF 模型是 BHB 模型的改进版,增加了基准收益 $R^{B}$ 对配置收益的影响,基本框架如下图所示,其中仍以红色渲染部分表示投资组合的超额收益。

BF 模型在配置效应部分的计算引入了基准收益 $R^{B}$,新的配置效应可以表示为: $$ AR_{BF}=\sum_{i=1}^{I}(w_{i}^{P} - w_{i}^{B})(r_{i}^{B} - R^{B}) $$
由于资产组合权重 $w_{i}^{P}$ 和基准组合权重 $w_{i}^{B}$ 加总均为 1,而 $R^{B}$ 是一个常数,因此: $$ \begin{gather*} \sum_{i=1}^{I}(w_{i}^{P} - w_{i}^{B})R^{B} = 0 \cr AR_{BHB} = \sum_{i=1}^{I}(w_{i}^{P} - w_{i}^{B})r_{i}^{B} = \sum_{i=1}^{I}(w_{i}^{P} - w_{i}^{B})(r_{i}^{B} - R^{B}) = AR_{BF} \end{gather*} $$
也就是说,相较于 BHB 模型而言,BF 模型中对于基准收益的引入并不会改变其配置效应的大小,二者是完全等同的,但在直观解释上 BF 模型却与投资者的实际操作更为贴合,它认为:只有超配那些相较基准指数具有正向超额收益的行业、低配那些相较基准指数具有负向超额收益的行业,才能算是成功的行业配置策略。
BF 模型还将 BHB 模型中的选择效应和交互效应进行了合并,形成新的选股效应: $$ \begin{align*} SR_{BF} &= SR_{BHB} + IR_{BHB} \cr &= \sum_{i=1}^{I}w_{i}^{B}(r_{i}^{P} - r_{i}^{B}) + \sum_{i=1}^{I}(w_{i}^{P} - w_{i}^{B})(r_{i}^{P} - r_{i}^{B}) \cr &= \sum_{i=1}^{I}w_{i}^{P}(r_{i}^{P} - r_{i}^{B}) \end{align*} $$
最后,BF 模型就将投资组合的超额收益 $R^{A}$ 分解到了对行业的配置效应 $AR$ 和行业内部的选股效应 $SR$ 两个部分: $$ \begin{equation*} R^A_{BF} = AR_{BF} + SR_{BF} = \sum\limits_{i=1}^{I}(w_i^P - w_i^B)(r_i^B - R^B) + \sum\limits_{i=1}^{I}w_i^P(r_i^P - r_i^B) \end{equation*} $$
下面,我们开始
Reference: 《“星火”多因子专题报告(四) —— 基于持仓的基金业绩归因:始于 Brinson,归于 Barra》,财通证券。
